There are a number of issues with the raw COVID-19 statistical data. Most, if not all, of them come from the fact that different countries use different methods to get the numbers.
The covid.observer site aims to display the data to reduce panic, and it strongly needs data about recoveries.
Unfortunately, the underlying data set is suffering from the lack of such data in the official sources. The Dutch ministry of health, for example, gives detailed daily updates but there’re no mentions of recoveries.
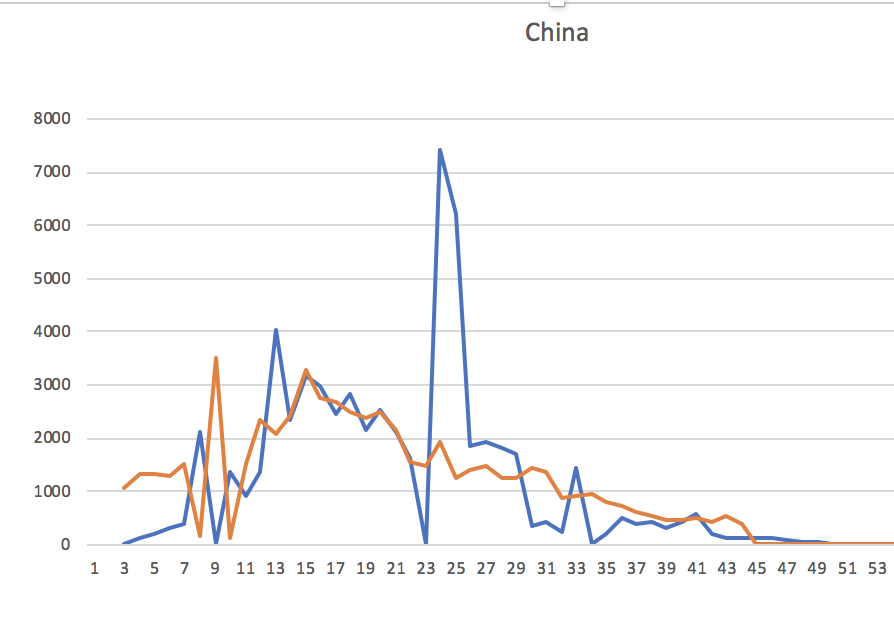
The fact is that the majority of people do recover (look at China), and this is a crucial point to understand the general danger of the whole coronavirus story.
I tried to and reveal the number of recoveries for the countries where we have no data. The idea is that any confirmed case has two outputs: a person either recovers or dies. It would be a huge simplification, but let me first assume that every infected person either dies in f days or recovers in r days.
Thus, for any given day n, the growth of confirmed cases is a sum of the changes in deaths that happen in f days and the number of recoveries after r days:
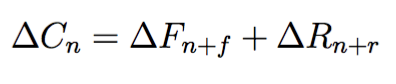
The per-day deltas for the confirmed C cases and the deltas for deaths F can be easily obtained from the source data for each country. What ones need to do is to find such f and r so that the deltas agree with existing data.
Knowing the number of confirmed cases and the number of failures, we could estimate the number of recoveries per day.
In the case of Italy and China’s province Hubei, we have all three series of data. A simple modelling gave me the following numbers for them:
| Country | Days to die | Days to recover |
| Italy | 9 | 13 |
| China/Hubei | 10 | 25 |
Let us compare the real confirmed cases changes per day with the approximation based on the above computations. The blue line is actual delta, the orange line is computed based on the above formula.
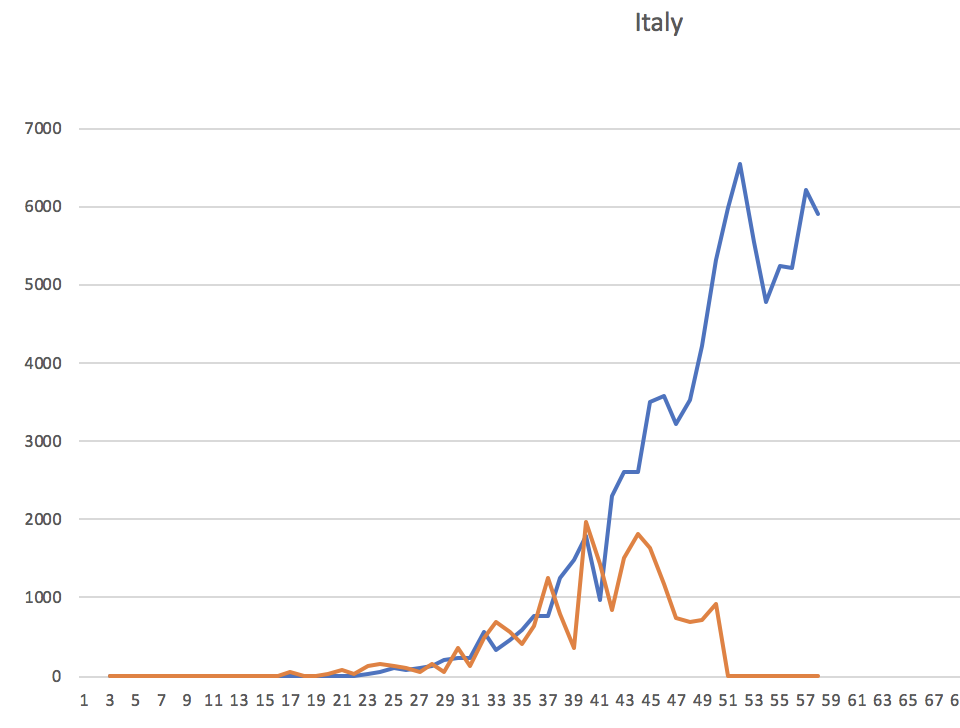
Just have in mind that as the story in Italy is not yet over, we only can project data not later than two weeks from today.
It is also quite visible and understandable that to be considered recovered, a person can be tested either after 14 days, or after 21, or even if they did not die within a month, — but any number helps presenting the recovery graphs less panicking and reflecting the truth, even if the real number of days to recover varies a lot or if they are delayed.
I wrote a program that brute forces the two parameters to grasp some idea of common values of f and r, which could be applied to the numbers for the Netherlands, in particular.
As it often happens, as soon as I got the numbers, the JHS’s dashboard started displaying the number of recoveries for the Netherlands:

Let us thus wait until tomorrow to see the update on the site.