In this post, I’d like to demonstrate a few ways of computing factorials using the Raku programming language.
1 — reduction
Let me start with the basic and the most effective (non necessarily the most efficient) form of computing the factorial of a given integer number:
say [*] 1..10; # 3628800
In the below examples, we mostly will be dealing with the factorial of 10, so remember the result. But to make the programs more versatile, let us read the number from the command line:
unit sub MAIN($n); say [*] 1..$n;
To run the program, pass the number:
$ raku 00-cmd.raku 10 3628800
The program uses the reduction meta-operator [ ] with the main operator * in it.
You can also start with 2 (you can even compute 0! and 1! this way).
unit sub MAIN($n); say [*] 2..$n;
2 — for
The second solution is using a postfix for loop to multiply the numbers in the range:
unit sub MAIN($n); my $f = 1; $f *= $_ for 2..$n; say $f;
This solution is not that expressive but still demonstrates quite a clear code.
3 — map
You can also use map that is applied to a range:
unit sub MAIN($n); my $f = 1; (2..$n).map: $f *= *; say $f;
Refer to my article All the stars of Perl 6, or * ** * to learn more about how to read *= *.
4 — recursion
Let’s implement a recursive solution.
unit sub MAIN($n);
sub factorial($n) {
if $n < 2 {
return 1;
}
else {
return $n * factorial($n - 1);
}
}
say factorial(n);
There are two branches, one of which terminates recursion.
5 — better recursion
The previous program can be rewritten to make a code with less punctuation:
unit sub MAIN($n);
sub factorial($n) {
return 1 if $n < 2;
return $n * factorial($n - 1);
}
say factorial($n);
Here, the first return is managed by a postfix if, and the second return can only be reached if the condition in if is false. So, neither an additional Boolean test nor else is needed.
6 — big numbers
What if you need to compute a factorial of a relatively big number? No worries, Raku will just do it:
say [*] 1..500;
The speed is more than acceptable for any practical application:
raku 06-long-factorial.raku 0.14s user 0.02s system 124% cpu 0.127 total
7 — small numbers
Let’s try something opposite and compute a factorial, which can fit a native integer:
unit sub MAIN($n); my int $f = 1; $f *= $_ for 2..$n; say $f;
I am using a for loop here, but notice that the type of $f is a native integer (thus, 4 bytes). This program works with the numbers up to 20:
$ raku 07-int-factorial.raku 20 2432902008176640000
8 — sequence
The fun fact is that you can add a dot to the first program 🙂
unit sub MAIN($n); say [*] 1 ... $n;
Now, 1 ... $n is a sequence. You can start it with 2 if you are not planning to compute a factorials of 0 and 1.
9 — reversed sequence
Unlike the solution with a range, it is possible to swap the ends of the sequence:
unit sub MAIN($n); say [*] $n ... 1;
10 — sequence with definition
Nothing stops us from defining the elements of the sequence with a code block. The next program shows how you do it:
unit sub MAIN($n); my @f = 1, * * ++$ ... *; say @f[$n];
This time, the program generates a sequence of factorials from 1! to $n!, and to print the only one we need, we take the value from the array as @f[$n]. Notice that the sequence itself is lazy and its right end is undefined, so you can’t use @f[*-1], for example.
The rule here is * * ++$ (multiply the last computed value by the incremented index); it is using the built-in state variable $.
11 — multi functions
The idea of the solutions 4 and 5 with two branches can be further transformed to using multi-functions:
unit sub MAIN($n);
multi sub factorial(1) { 1 }
multi sub factorial($n) { $n * factorial($n - 1) }
say factorial($n);
For the numbers above 1, Raku calls the second variant of the function. When the number comes down to 1, recursion stops, because the first variant is called. Notice how easily you can create a variant of a function that only reacts to the given value.
12 — where
The previous program loops infinitely if you try to set $n to 0. One of the simplest solution is to add a where clause to catch that case too.
unit sub MAIN($n);
multi sub factorial($n where $n < 2) { 1 }
multi sub factorial($n) { $n * factorial($n - 1) }
say factorial($n);
13 — operator
Here’s another classical Raku solution: modifying its grammar to allow mathematical notation $n!.
unit sub MAIN($n);
sub postfix:<!>($n) {
[*] 1..$n
}
say $n!;
14 — methodop
A rarely seen Raku’s feature called methodop (method operator) that allows you to call a function as it if was a method:
unit sub MAIN($n);
sub factorial($n) {
[*] 1..$n
}
say $n.&factorial;
15 — cached
Recursive solutions are perfect subjects for result caching. The following program demonstrates this approach.
unit sub MAIN($n);
use experimental :cached;
sub f($n) is cached {
say "Called f($n)";
return 1 if $n < 2;
return $n * f($n - 1);
}
say f($n div 2);
say f(10);
This program first computes a factorial of the half of the input number, and then of the number itself. The program logs all the calls of the function. You can clearly see that, say, the factorial of 10 is using the results that were already computed for the factorial of 5:
$ raku 15-cached-factorial.raku 10 Called f(5) Called f(4) Called f(3) Called f(2) Called f(1) 120 Called f(10) Called f(9) Called f(8) Called f(7) Called f(6) 3628800
Note that the feature is experimental.
16 — triangular reduction
The reduction operator that we already used has a special variant [\ ] that allows to keep all the intermediate results. This is somewhat similar to using a sequence in the example 10.
unit sub MAIN($n); my @f = [\*] 1..$n; say @f[$n - 1];
17 — division of factorials
Now a few programs that go beyond the factorials themselves. The first program computes the value of the expression a! / b!, where both a and b are integer numbers, and a is not less than b.
The idea is to optimise the solution to skip the overlapping parts of the multiplication sequences. For example, 10! / 5! is 6 * 7 * 8 * 9 * 10.
To have more fun, let us modify Raku’s grammar so that it really parses the above expression.
unit sub MAIN($a, $b where $a >= $b);
class F {
has $.n;
}
sub postfix:<!>(Int $n) {
F.new(n => $n)
}
sub infix:</>(F $a, F $b) {
[*] $b.n ^.. $a.n
}
say $a! / $b!;
We already have seen the postfix:<!> operator. To catch division, another operator is defined, but to prevent catching the division of data of other types, a proxy class F is introduced.
To keep proper processing of expression such as 4 / 5, define another / operator that catches things which are not F. Don’t forget to add multi to both options. The callsame built-in routine dispatches control to built-in operator definitions.
. . .
multi sub infix:</>(F $a, F $b) {
[*] $b.n ^.. $a.n
}
multi sub infix:</>($a, $b) {
callsame
}
say $a! / $b!;
say 4 / 5;
18 — optimisation
Let’s try to reduce the number of multiplications. Take a factorial of 10:
10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
Now, take one number from each end, multiply them, and repeat the procedure:
10 * 1 = 10 9 * 2 = 18 8 * 3 = 24 7 * 4 = 28 6 * 5 = 30
You can see that every such result is bigger than the previous one by 8, 6, 4, and 2. In other words, the difference reduces by 2 on each iteration, starting from 10, which is the input number.
The whole program that implements this algorithm is shown below:
unit sub MAIN(
$n is copy where $n %% 2 #= Even numbers only
);
my $f = $n;
my $d = $n - 2;
my $m = $n + $d;
while $d > 0 {
$f *= $m;
$d -= 2;
$m += $d;
}
say $f;
It only works for even input numbers, so it contains a restriction reflected in the where clause of the MAIN function. As homework, modify the program to accept odd numbers too.
19 — integral
Before wrapping up, let’s look at a couple of exotic methods, which, however, can be used to compute factorials of non-integer numbers (or, to be stricter, to compute what can be called extended definition of it).
The proper way would be to use the Gamma function, but let me illustrate the method with a simpler formula:
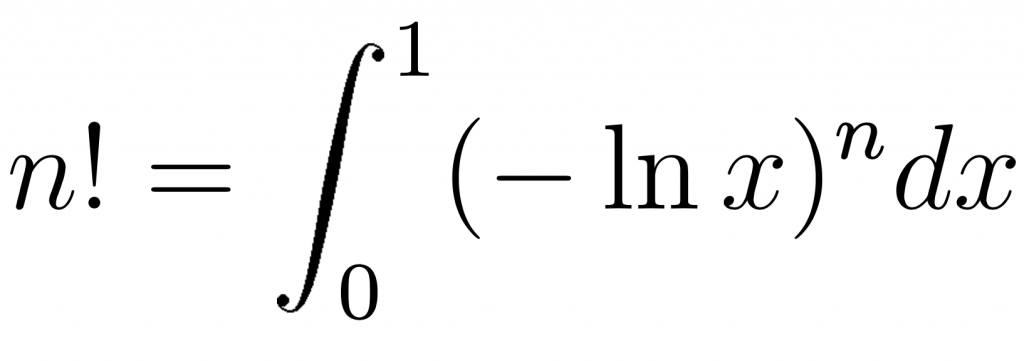
An integral is a sum by definition, so let’s make a straightforward loop:
unit sub MAIN($n);
my num $f = 0E0;
my num $dx = 1E-6;
loop (my $x = $dx; $x <= 1; $x += $dx) {
$f += (-log($x)) ** $n;
}
say $f * $dx;
With the given step of 1E-6, the result is not that exact:
$ raku 19-integral-factorial.raku 10 3086830.6595557937
But you can compute a ‘factorial’ of a floating-point number. For example, 5! is 120 and 6! is 720, but what is 5.5!?
$ raku 19-integral-factorial.raku 5.5 285.948286477563
20 — another formula
And finally, the Stirling’s formula for the rescue. The bigger the n, the more correct is the result.
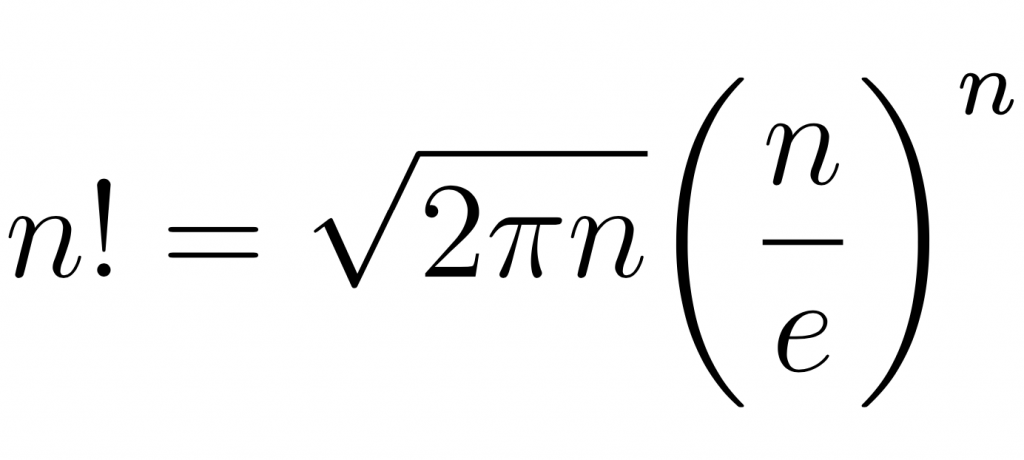
The implementation can be as simple as this:
unit sub MAIN($n); # τ = 2 * π say (τ * $n).sqrt * ($n / e) ** $n;
But you can make it a bit more outstanding if you have a fixed $n:
say sqrt(τ * 10) * (10 / e)¹⁰;
* * *
And that’s it for now. You can find the source code of all the programs shown here in the GitHub repository github.com/ash/factorial.
my @fac = lazy gather { my $f = 1; take $f; take $f *= $_ for 1..*; }