Today, we continue working with the Bridge method in Rakudo Perl 6. Yesterday, we saw the definitions of the methods in a few pre-defined data types. It is time to see how the method is used.
What’s inside?
The major use of the method is inside the Real role, which contains the following set of methods:
method sqrt() { self.Bridge.sqrt }
method rand() { self.Bridge.rand }
method sin() { self.Bridge.sin }
method asin() { self.Bridge.asin }
method cos() { self.Bridge.cos }
method acos() { self.Bridge.acos }
method tan() { self.Bridge.tan }
method atan() { self.Bridge.atan }
. . .
method sec() { self.Bridge.sec }
method asec() { self.Bridge.asec }
method cosec() { self.Bridge.cosec }
method acosec() { self.Bridge.acosec }
method cotan() { self.Bridge.cotan }
method acotan() { self.Bridge.acotan }
method sinh() { self.Bridge.sinh }
method asinh() { self.Bridge.asinh }
method cosh() { self.Bridge.cosh }
method acosh() { self.Bridge.acosh }
method tanh() { self.Bridge.tanh }
method atanh() { self.Bridge.atanh }
method sech() { self.Bridge.sech }
method asech() { self.Bridge.asech }
method cosech() { self.Bridge.cosech }
method acosech() { self.Bridge.acosech }
method cotanh() { self.Bridge.cotanh }
method acotanh() { self.Bridge.acotanh }
method floor() { self.Bridge.floor }
method ceiling() { self.Bridge.ceiling }
. . .
multi method log(Real:D: ) { self.Bridge.log }
multi method exp(Real:D: ) { self.Bridge.exp }
There are a few routines with a different pattern, where the method is called twice: once for getting to the needed function; second to coerce the value:
multi method atan2(Real $x = 1e0) { self.Bridge.atan2($x.Bridge) }
multi method atan2(Cool $x = 1e0) { self.Bridge.atan2($x.Numeric.Bridge) }
multi method atan2(Real $x = 1e0) { self.Bridge.atan2($x.Bridge) }
multi method atan2(Cool $x = 1e0) { self.Bridge.atan2($x.Numeric.Bridge) }
multi method log(Real:D: Real $base) { self.Bridge.log($base.Bridge) }
. . .
multi sub atan2(Real \a, Real \b = 1e0) { a.Bridge.atan2(b.Bridge) }
As you see, the atan2 function is defined both as a method and as a subroutine. To confuse you a bit more, there are two versions of it:
proto sub atan2($, $?) {*}
multi sub atan2(Real \a, Real \b = 1e0) { a.Bridge.atan2(b.Bridge) }
# should really be (Cool, Cool), and then (Cool, Real) and (Real, Cool)
# candidates, but since Int both conforms to Cool and Real, we'd get lots
# of ambiguous dispatches. So just go with (Any, Any) for now.
multi sub atan2( \a, \b = 1e0) { a.Numeric.atan2(b.Numeric) }
Finally, a couple of methods for type conversions:
method Bridge(Real:D:) { self.Num }
method Int(Real:D:) { self.Bridge.Int }
method Num(Real:D:) { self.Bridge.Num }
multi method Str(Real:D:) { self.Bridge.Str }
method Rat(Real:D: Real $epsilon = 1.0e-6) { self.Bridge.Rat($epsilon) }
Notice that the Bridge method of the Real role returns a Num value.
Some infix methods are also using the method in hand:
multi sub infix:<+>(Real \a, Real \b) { a.Bridge + b.Bridge }
multi sub infix:<->(Real \a, Real \b) { a.Bridge - b.Bridge }
multi sub infix:<*>(Real \a, Real \b) { a.Bridge * b.Bridge }
multi sub infix:</>(Real \a, Real \b) { a.Bridge / b.Bridge }
multi sub infix:<%>(Real \a, Real \b) { a.Bridge % b.Bridge }
multi sub infix:<**>(Real \a, Real \b) { a.Bridge ** b.Bridge }
multi sub infix:«<=>»(Real \a, Real \b) { a.Bridge <=> b.Bridge }
multi sub infix:<==>(Real \a, Real \b) { a.Bridge == b.Bridge }
multi sub infix:«<»(Real \a, Real \b) { a.Bridge < b.Bridge }
multi sub infix:«<=»(Real \a, Real \b) { a.Bridge <= b.Bridge }
multi sub infix:«≤» (Real \a, Real \b) { a.Bridge ≤ b.Bridge }
multi sub infix:«>»(Real \a, Real \b) { a.Bridge > b.Bridge }
multi sub infix:«>=»(Real \a, Real \b) { a.Bridge >= b.Bridge }
multi sub infix:«≥» (Real \a, Real \b) { a.Bridge ≥ b.Bridge }
multi sub prefix:<->(Real:D \a) { -a.Bridge }
Trace the calls
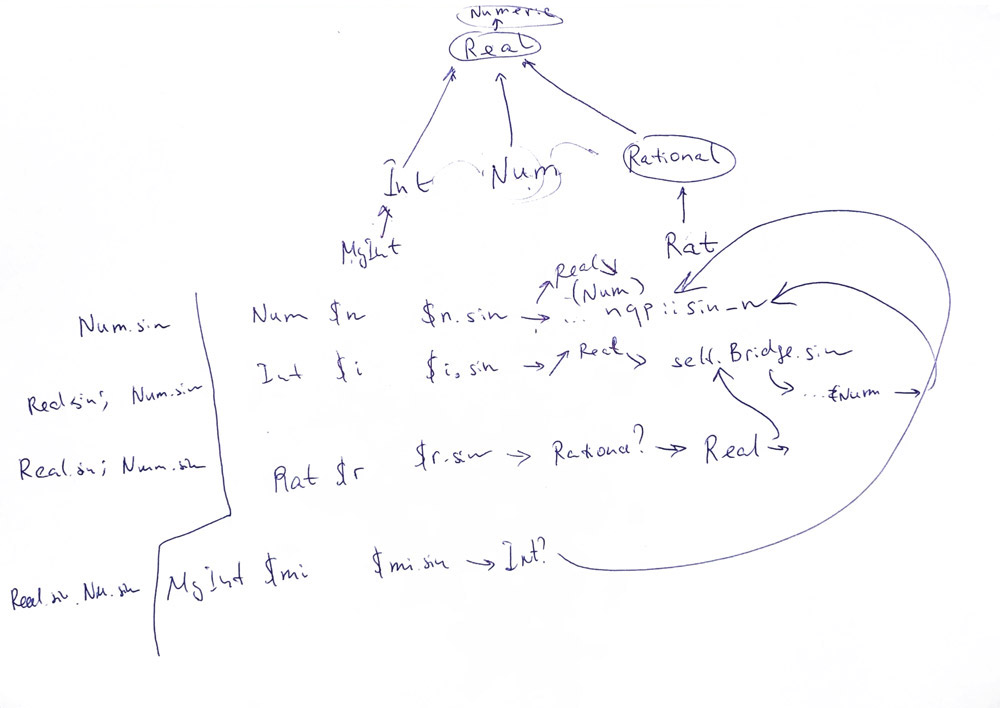
To see when the Bridge method is called, let us do a few simple experiments. I added a few nqp::say calls and run the REPL console to invoke a sin method on the variables of different types.
With the Num data type, a direct method is called:
> my Num $n = 1e1; 10 > $n.sin Num.sin
This method is calling the underlying NQP function:
proto method sin(|) {*}
multi method sin(Num:D: ) {
nqp::p6box_n(nqp::sin_n(nqp::unbox_n(self)));
}
With other data types, you travel via the Real role:
> my Int $i = 1; 1 > $i.sin Real.sin Num.sin > my Rat $r = 1/2; 0.5 > $r.sin Real.sin Num.sin
The same path you experience with your own types, if they are inherited from the built-in ones:
> class MyInt is Int {}
> my MyInt $mi = MyInt.new
0
> $mi.sin
Real.sin
Num.sin
Get rid of it
I revised all the places where the method was used in my clone of Rakudo. Mostly, they are replaced with a direct call of the Num method. In a few places it leads to double calls like $x.Num.Num, which were also reduced, of course.
With the updated code, all the tests from Roast were passed. As a side effect, the speed in some cases is increased by around 3%:
./perl6 -e'for 1..10_000_000 {Int.new(1).sin}'
It is quite an extensive change, and still, there is one thing left: the thing that causes an infinite loop when you call the method on a newly created Real object. It looks like the wrong hierarchy of the numerical data types is the main cause, but I assume that we can safely remove the Bridge method at least.
Update. They core developers (although at first not clearly understanding why it the method was needed at all) decided to keep the method and updated the documentation, which is also a positive output 🙂
One thought on “🔬54. Going over the Bridge, part 2. Let’s get rid of it”