🔬41. Converting Num to Rat in Raku

In Perl 6, you can easily coerce numerical values from one type to another. One of the interesting conversions is Num to Rat.

For example, take the value of π and convert it to a fraction:

$ perl6 -e'say pi.Rat.perl'
<355/113>

Indeed, 355/113 is 3.14159292035398, which is close to π. The default maximum error is built-in in Rakudo and is set to 10^–6.

Algorithm

The implementation of the method is located in the src/core/Num.pm file. Let us read it line by line. First, the signature:

method Rat(Num:D: Real $epsilon = 1.0e-6, :$fat)

Here, you see $epsilon, a positional parameter with the default value, and a flag, :$fat, which you should set if you want to have a FatRat value. The first action is creating a variable that is either a Rat or a FatRat:

 my \RAT = $fat ?? FatRat !! Rat;

The next step is a test whether the number is a number and is not infinite:

 return RAT.new: (
     nqp::iseq_n(self, self) ?? nqp::iseq_n(self, Inf) ?? 1 !! -1 !! 0
   ), 0
 if nqp::isnanorinf(nqp::unbox_n(self));

Another quick check — return immediately if the value is already an integer:

my Num $num = self;
$num = -$num if (my int $signum = $num < 0);
my num $r = $num - floor($num);

if nqp::iseq_n($r,0e0) {
    RAT.new(nqp::fromnum_I(self,Int),1)
}

At this point, we have a first approximation: the $num variable contains an integer part. The rest is shown in the picture:

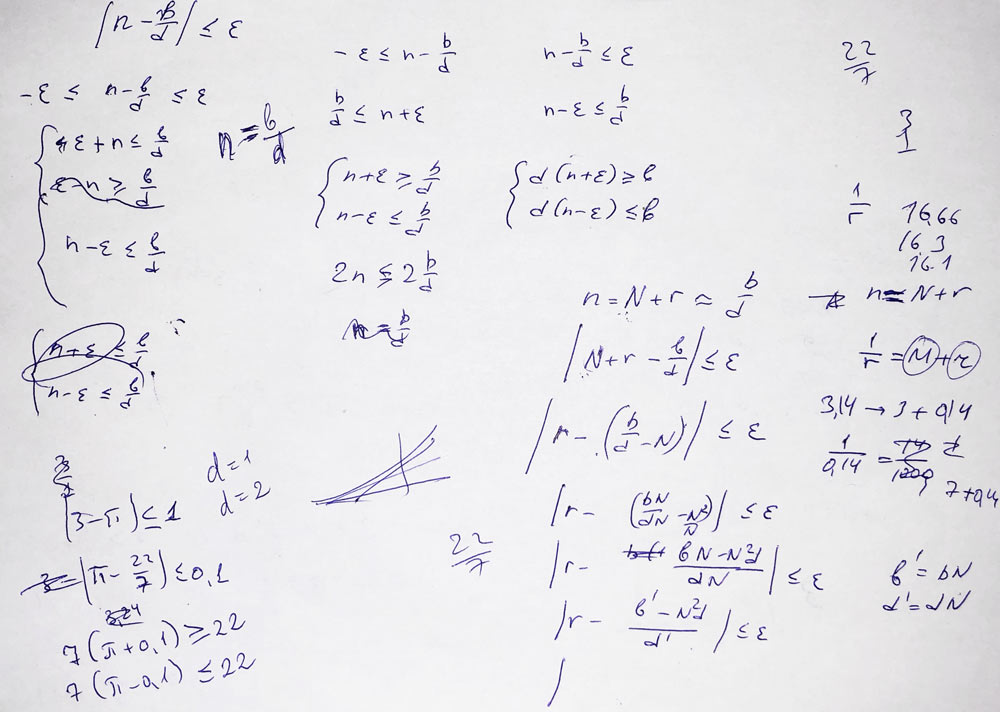
Seriously speaking, the rest of the method is an implementation of the numerical approximation, which tries to find such numerator and denominator so that the fraction is close enough to the value in question.

First, some values are initialised and prepared:

 my Int $q = nqp::fromnum_I($num, Int);
 my Int $a = 1;
 my Int $b = $q;
 my Int $c = 0;
 my Int $d = 1;

Now, $q and $b (which is the numerator) are the most rough integer approximation, and $d (denominator) is set to 1.

The rest is a loop, which stops when an accurate enough fraction is found:

while nqp::isne_n($r,0e0) && abs($num - ($b / $d)) > $epsilon {
    my num $modf_arg = 1e0 / $r;
    $q = nqp::fromnum_I($modf_arg, Int);
    $r = $modf_arg - floor($modf_arg);

    my $orig_b = $b;
    $b = $q * $b + $a;
    $a = $orig_b;

    my $orig_d = $d;
    $d = $q * $d + $c;
    $c = $orig_d;
}

And finally, a Rat value is built:

RAT.new($signum ?? -$b !! $b, $d)

Approximation

When using the Num::Rat method, as we saw, you can set the precision you need. For example:

$ ./perl6 -e'say pi.Rat(1)'
3

$ ./perl6 -e'say pi.Rat(0.1)'
3.142857

I also added some debug output to see the steps that the algorithm comes through. Surprisingly, it converges very quickly.

$ ./perl6 -e'say pi.Rat.nude'
3/1 = 3
22/7 = 3.142857
333/106 = 3.141509
(355 113)

$ ./perl6 -e'say pi.Rat(1e-10).nude'
3/1 = 3
22/7 = 3.142857
333/106 = 3.141509
355/113 = 3.141593
103993/33102 = 3.141593
104348/33215 = 3.141593
208341/66317 = 3.141593
(312689 99532)

$ ./perl6 -e'say e.Rat.nude'
2/1 = 2
3/1 = 3
8/3 = 2.666667
11/4 = 2.75
19/7 = 2.714286
87/32 = 2.71875
106/39 = 2.717949
193/71 = 2.718310
1264/465 = 2.718280
1457/536 = 2.718284
(2721 1001)