Raku challenge Week 69, issue 2

The second task of this week’s challenge is to generate the N^th element in the sequence that is defined via a recurrent formula, which I will directly express in Raku:

multi sub S(0) {''}
multi sub S(1) {'0'}
multi sub S($n) {
    my $prev = S($n - 1);
    $prev ~ '0' ~ $prev.flip.trans('01' => '10')
}

At first, you may think it is a perfect match for Raku’s multi-functions, and it really is unless you read the next requirement from the task: Generate S1000. That is a bit too optimistic 🙂 (Update: it is asked to generate S30 now.)

First, let us run the program for the first few generations:

say "S$_ = {S($_)}" for ^9;

The program prints the following lines in just a fraction of a second:

$ time raku ch-2.raku 
S0 = 
S1 = 0
S2 = 001
S3 = 0010011
S4 = 001001100011011
S5 = 0010011000110110001001110011011
S6 = 001001100011011000100111001101100010011000110111001001110011011
S7 = 0010011000110110001001110011011000100110001101110010011100110110001001100011011000100111001101110010011000110111001001110011011
S8 = 001001100011011000100111001101100010011000110111001001110011011000100110001101100010011100110111001001100011011100100111001101100010011000110110001001110011011000100110001101110010011100110111001001100011011000100111001101110010011000110111001001110011011
 
real 0m0.351s
user 0m0.224s
sys 0m0.068s

If you call S(1000), you will never get a result, and that’s not because Raku is not fast enough.

Here is the graph showing how the string grows in size depending on generation number:

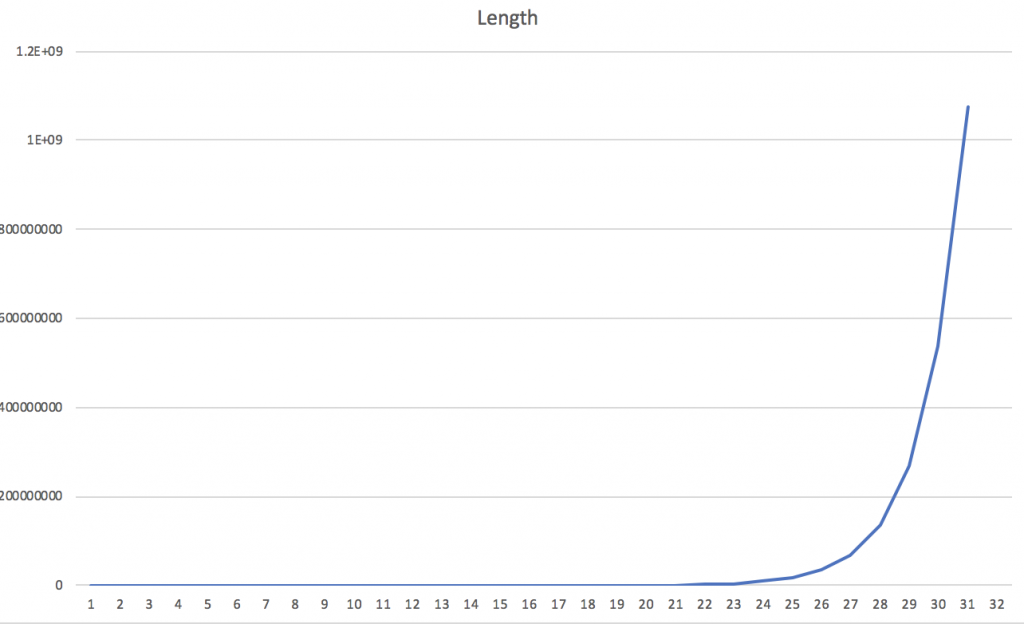
It is an exponential growth of O(2^N).

Nevertheless, we can try optimising the first program.

Let us analyse the algorithm once again by looking at the first elements of the sequence.

S2 = 001
S3 = 0010011
S4 = 001001100011011
S5 = 0010011000110110001001110011011

The already-generated part of the string never changes. The left part of the current string always repeats the previous one. So, there is no need to create new strings on each iteration. What we really need, is to append the new bits to the end of the string.

I would let you try real bit operations as homework but propose a simple proof-of-concept solution with native ints instead.

my @bits of int;
@bits.push(0);

for ^9 -> $n {
    my $size = @bits.elems;
    print "S{$n+2} = ";
    @bits.push(0);
    @bits.push(@bits[$size - $_] ?? 0 !! 1) for 1 .. $size;

    .print for @bits;
    ''.say;
}

Compare the two programs for, say, N = 25 (remove any printing instructions to not spend time on output):

$ time ch-2.raku

real 0m42.401s
user 0m36.209s
sys 0m5.744s
 

$time ch-2-bits.raku

real 0m11.561s
user 0m11.296s
sys 0m0.331s

No doubts the second program is faster.

But before wrapping up, let me re-write the program in C++ and use an std::vector<bool> to keep the result (that’s not that necessary, as we still are not able to generate S1000).

#include <iostream>
#include <vector>

using namespace std;

int main() {
    vector<bool> bits;
    bits.push_back(0);

    for (int n = 0; n <= 9; n++) {
        int size = bits.size();
        bits.push_back(0);

        cout << 'S' << (n + 2) << " = ";

        for (int m = 1; m <= size; m++)
            bits.push_back(!bits[size - m]);

        for (auto x : bits) cout << x;
        cout << endl;
    }
}

(That’s always a pleasure to see how fast C++ programs are.)

Let me not post the value of S30 here as its length is about 1 GB (1,073,741,823 to be correct).

And that’s all for now. See you next Monday.

Update: read a continuation with another interesting solution that uses Raku’s sequences.

→ GitHub repository
→ Navigation to the Raku challenges post series